ブラックジャックの現状と基本戦略

ブラックジャックはカジノゲームの中でも最も人気の高いテーブルゲームで、毎年900億ドル近くが賭けられていると言われています。アメリカの人口から考えて1人当たり毎年275ドルも賭けているのです。

しかし結果は残念ながら思わしいものではなく、毎年20億ドルほどカジノ側が勝っているというのが現状です。

ブラックジャック攻略と言えばまずカードカウンティングが思い浮かばれますが、ここではそれ以前に遡り、基本戦略を見ていこうと思います。

基本戦略(ベーシックストラテジー)というのは、残りのデッキの状態に関係なく、プレイヤーの最初の2枚のハンドと、ディーラーのアップカード(最初の表向きのカード)から、期待値に基づいた最善のアクションを取っていく戦略になります。

カードカウンティングがゲーム間が従属事象なのに対して、基本戦略は独立事象ということになります。

 

基本戦略の歴史

1950年代当時のブラックジャックプレイヤーのプレイはとてもお粗末なもので、12や13でのヒットは普通、8のスプリットはほとんど見られずスプリットされるものは10が多い、A5などのソフトトータルでのダブルはまず見られない、といったものでした。

1953年になってボールドウィン、カンティー、マイゼル、マクダーモットの4人の陸軍数学者がブラックジャックの研究をはじめ、3年間の膨大な計算結果を元に発表されたのが基本戦略(ベーシックストラテジー)というものです。『Journal of the American Statistical Association』の「The Optimum Strategy in Blackjack」の中でoptimum strategyとして紹介しています。

これはとても優秀でシングルデッキでは期待値は0%(トントン)になるまでに至りました。それまで最も最適な戦略でも－3.6%だったので飛躍的な向上と言えます。発売当時その本を手に取ったソープ教授がラスベガスの旅行中に実践検証してみたら、初期投資は消えなかったという結果になっています。

 

その後何人もの人がプレイを検証し、設定やルールに対応していき、いくつもの基本戦略が生まれましたが、そのほとんどはシングルデッキかマルチデッキ対応のものでした。どの基本戦略でも誤差は0.03%と非常に小さいです。ここではシングルからマルチデッキまで全てに汎用できる戦略を紹介します。

 

汎用基本戦略

使用されるカードがランダムでカウンティング等の情報がない時、これに従うことにより最もプレイヤーの成績を高めてくれる戦略。期待値0%で理論上はほぼトントンになります。

			ディーラーのアップカード
			2	3	4	5	6	7	8	9	10	A
プレイヤーのハンド	スプリット	A-A	Sp	Sp	Sp	Sp	Sp	Sp	Sp	Sp	Sp	Sp
		10-10	S	S	S	S	S	S	S	S	S	S
		9-9	Sp	Sp	Sp	Sp	Sp	S	Sp	Sp	S	S
		8-8	Sp	Sp	Sp	Sp	Sp	Sp	Sp	Sp	Sp	Sp
		7-7	Sp	Sp	Sp	Sp	Sp	Sp	H	H	H	H
		6-6	H	Sp	Sp	Sp	Sp	H	H	H	H	H
		5-5	D	D	D	D	D	D	D	D	H	H
		4-4	H	H	H	H	H	H	H	H	H	H
		3-3	H	H	Sp	Sp	Sp	Sp	H	H	H	H
		2-2	H	H	Sp	Sp	Sp	Sp	H	H	H	H
	ハードハンド	H17↑	S	S	S	S	S	S	S	S	S	S
		H16	S	S	S	S	S	H	H	Su/H	Su/H	Su/H
		H15	S	S	S	S	S	H	H	H	Su/H	H
		H14	S	S	S	S	S	H	H	H	H	H
		H13	S	S	S	S	S	H	H	H	H	H
		H12	H	H	S	S	S	H	H	H	H	H
		11	D/H	D/H	D/H	D/H	D/H	D/H	D/H	D/H	D/H	H
		10	D/H	D/H	D/H	D/H	D/H	D/H	D/H	D/H	H	H
		9	H	D/H	D/H	D/H	D/H	H	H	H	H	H
		8↓	H	H	H	H	H	H	H	H	H	H
	ソフトハンド	S19↑	S	S	S	S	S	S	S	S	S	S
		S18	S	D/S	D/S	D/S	D/S	S	S	H	H	H
		S17	H	D/H	D/H	D/H	D/H	H	H	H	H	H
		S16	H	H	D/H	D/H	D/H	H	H	H	H	H
		S15	H	H	D/H	D/H	D/H	H	H	H	H	H
		S14	H	H	H	D/H	D/H	H	H	H	H	H
		S13	H	H	H	D/H	D/H	H	H	H	H	H

Sp：スプリット、S：スタンド、H：ヒット、D：ダブル、Su：サレンダー、Su/H：サレンダー不可のルールではヒット、D/H：ダブル不可のルールではヒット、D/S：ダブル不可のルールではスタンド

※どんな場合でもインシュランスは取らない。

 

この基本戦略には以下の特徴があります。

スプリットに関しては主にディーラーのアップカードが弱い時(6以下)に行われ、Aのペアと8のペアは常にスプリットする。Aのペアは攻撃的な意味合いを持ち、8のペアは半端な16を避けるためのディフェンス的な意味合いを持つ。

4、5、10のペアはどんな場合でもスプリットしないが、これはハンドの価値を下げないため。

ダブルに関しては、プレイヤーが一枚引いて完成されたハンドの勝算が高めの時に行う。

ヒットとスタンドに関しては、プレイヤーがスティッフハンド(合計12～16)で、ディーラーのアップカードが強い時(7以上)は、ディーラーがパットハンド(17～21)になる可能性が高いとみなしてヒットする。逆に弱い時はディーラーがバーストしてくれることに期待してスタンドする。

 

実際は細かいルールによって期待値が微妙に変わるため、以下の条件に合わせて修正します。(初期値のベンチマークの－0.02%から修正)

ベンチマーク	－0.02%
ハーフデッキ	＋0.71%
2デッキ	－0.32%
4デッキ	－0.48%
6デッキ	－0.53%
8デッキ	－0.55%
プッシュではディーラーが勝つ	－9.34%
ナチュラルでは等倍で支払う	－2.32%
ナチュラルは2倍で支払う	＋2.32%
ディーラーがソフト17をヒット	－0.2%
2回以上スプリットができない	－0.03%
Aを2回以上スプリットできる	＋0.06%
ソフトハンドでダブルできない	－0.11%
ダブルは10か11のみ	－0.21%
ダブルは11のみ	－0.69%
スプリット後にダブル可能	＋0.13%
サレンダー有り	＋0.06%

ベンチマーク：ラスベガスストリップのゲームと言われるルールで、シングルデッキ、最初の2枚ならどんなハンドでもダブル可能、ペアAのスプリット後にはカードが1枚ずつ配られる、ディーラーはソフト17をスタンド、サレンダーなし。カードが1枚も出ていない状態のゲームでは期待値は－0.02%で、この状態から修正していけばよい。

 

この修正表で気づくことは、まずはデッキ数が多くなればなるほど期待値が下がるということです。これはシングルデッキの方が1枚取り出された後の残りのカードへの影響力が大きいため、デッキ数が増えるほどその有利差が母数によってかき消されてしまうためです。

例えばプレイヤーが4、6のカードでディーラーのアップカードが5の時、プレイヤーはAか10を引くことを望むと思いますが、シングルデッキの時は20/49(0.408 )の確率なのに対して8デッキの時は160/413(0.387)まで下がってしまいます。

そしてプッシュはディーラーの勝ちとするルールは最悪で、長期的に見てプレイヤーが勝つことはまず不可能と言えます。このルールはチャリティーイベント等でよく採用されます。

 

なぜインシュランスは取らないのか？

インシュランスは基本的にどの戦略でも取りません。なぜなら、インシュランスの結果自体はメインハンドになにも影響を及ぼさず、完全にサイドベットでその期待値は完全にマイナスだからです。

4/13(2)＋9/13(－1)＝－1/13

単純計算で1回インシュランスをやる毎に、インシュランス代の－1/13が無くなる計算になります。

※しかしカウンティングができる場合はデッキに10が多く残っている場合はインシュランスが有効になてきます。

 

この汎用基本戦略で重要な所は、感情や結果は一切交えず、忠実にこの通りにプレイするということです。例えば16対7が3回連続で出て、3回ともバーストに終わったとしても、次に16対7が出ればやはりヒットしなければいけないのです。長期的に正しいプレイをするということが重要なのです。

 

 

汎用基本戦略の実戦

それでは汎用基本戦略をエンパイアカジノで実践してみます。

これがエンパイアカジノのテーブルゲームのブラックジャックのルールです。

そしてラウンド毎にカードはシャッフルされます。

これに合わせて期待値を修正してみます。

－0.02－0.53－0.03＋0.13＝－0.45%となります。

つまりこれは100ドルベットすると0.45ドル無くなる計算で、1000ドルベットすると4.5ドル無くなる計算です。

では1ドル賭けで上表に従い1000ドルほど賭けてみます。

 

これが初期資金です。少し少ないですが、4.5ドルしか無くならない計算ですので、これで事足りるはずです。

 

第1戦目

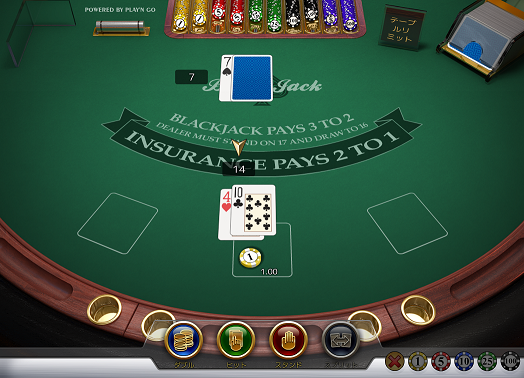
プレイヤーハード14対ディーラー7のアップカードです。上表に従いヒットします。

 

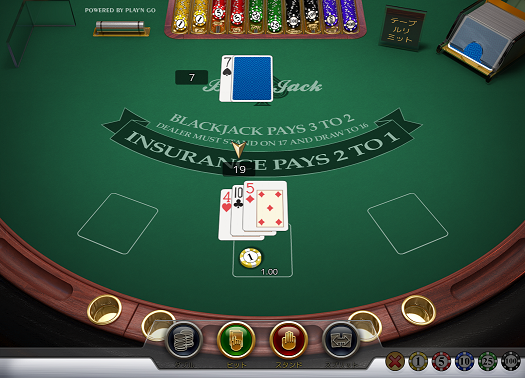
5を引いてハード19になりましたのでスタンドします。

 

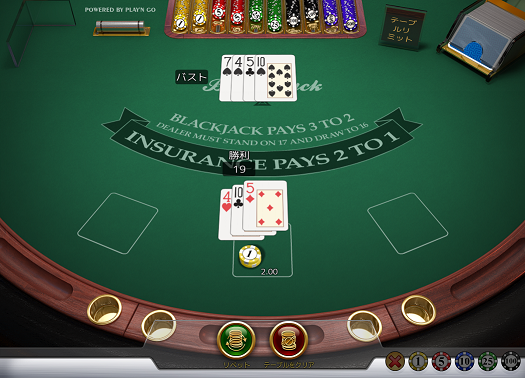
ディーラーは4、5、10と引いてバーストとなりプレイヤーの勝ちとなりました。

以下こんな感じで続けます。

 

第15戦目

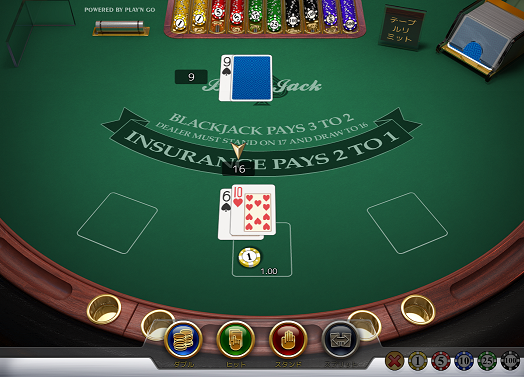
プレイヤーハード16対ディーラー9のアップカードで、上表に従ってヒットしなければなりませんが、16でヒットするのはやはり辛いところです。

 

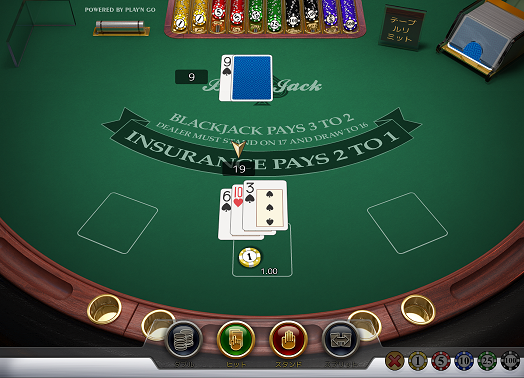
幸いにも引けたカードは3だったのですが・・・・

 

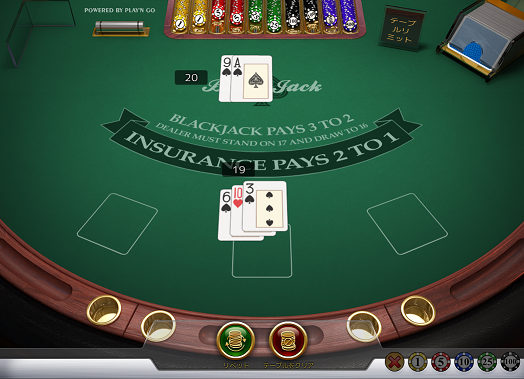
ディーラーの引いたカードはAで負けてしまいました。

 

以下は戦績表です。

いざ実践してみたのですが、最初は記入ミスが多く帳尻が合いませんでしたので、$65.33から改めて始めました。

$1ずつ賭け、ダブルは$2という計算です。

そして最終的には$58.33になりました。

65.33－58.33＝$7となり大体誤差の範囲だと思います。

 

単勝	304
単負	420
ダブ勝	47
ダブ負	23
プレイヤーBJ	38
プッシュ	80
スプリット回数	18

結果を集計しますとこんな感じになります。尚ミス(アクションによるもの)が4回ほどありましたが、2回負けて2回勝ったのでチャラとします。

 

以下はディーラーのアップカード毎のバースト数です。

2	20
3	20
4	30
5	25
6	28
7	11
8	11
9	18
10	37
A	3

アップカード10はT、J、Q、Kの4種類なので相対的なバースト数は9くらいだと思います。アップカード9でのバースト数は少し多いものの、大体6と7が境界で、アップカード7からバースト数が少なくなってることも分かります。そしてアップカードAになると極端にバーストしなくなることも分かります。

 

考察

やってみて気づいたことですが、やはりプレイヤーがバーストして負けるケースが圧倒的に多い感じがします。取り扱うハンドはほとんどがハードハンドですので、表のハードハンドの部分はやっていく中に覚えてしまいます。逆にダブルになった時は、負けよりも勝ちの方が圧倒的に多いです。これとプレイヤーのブラックジャックの1.5倍の配当でうまく帳尻があってるんだなという気がします。

$65.33が原点ですと、$80を超えたり、$40付近になってしまったりとこれくらいの変動幅はありました。

またこの実践を通して予想外に大きく負けたわけではないので、このゲームに仕組まれた意図といったものもないのがわかりました。

汎用基本戦略は決して勝てる戦略ではありませんが、これに従えば相当ゆっくり負けていくというのが分かりました。