ポンツーン(ポントゥーン)とは

カジノのテーブルゲームにはポンツーン(ポントゥーン)という、ブラックジャックと似て非なるゲームがあります。英語ではPontoonと書き、アメリカのブラックジャックをイギリスで改良したものです。リアルカジノではフィリッピンのカジノにあります。今回はこのポンツーンのルールと特徴、ブラックジャックとの違いをまとめてみたいと思います。ほとんどブラックジャックですが、まずはゲームの流れに沿ってルールを説明します。

 

ルール

基本的にはプレイヤーとディーラー(カジノ側)の対戦で、先に2枚づつカードを配り、追加でカードを引いて21に近づけた方が勝ちです。Aは1にも11にもなり、2～9はその数、TJQKは10としてカウントします。21を超えればバーストします。

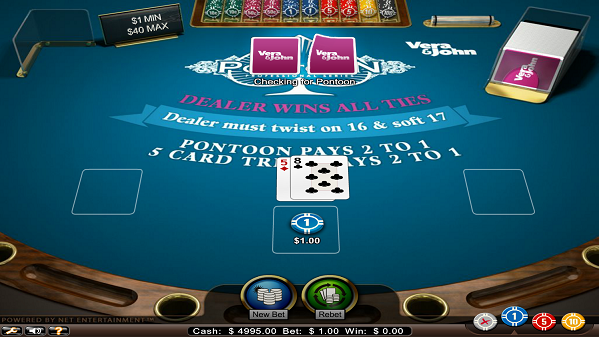
チップを置いてディールするとカードが2枚ずつ配られます。プレイヤーは2枚のカードが表向きですが、ディーラーは裏向きです。そしてディラーは自分のカードがポンツーン(Aを含んだ合計21)であるかどうか確認します。ポンツーンであれば即ディーラーの勝ちとなります。よってブラックジャックでいうサレンダーやインシュランスという概念はありません。もしプレイヤーがポンツーンでディーラーがそれ以外の場合はプレイヤーの勝ちで2倍の配当を受けることになります。(ブラックジャックの場合1.5倍。)両者がポンツーンの場合はディーラーの勝ちです。

 

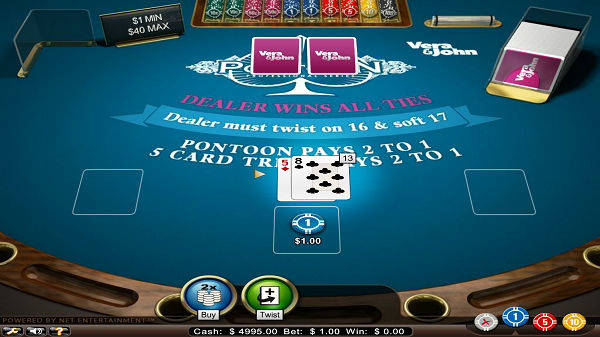
両者がポンツーンでなければ次のアクションに進みます。プレイヤーはバイかツイスト、スティック、スプリットを選択します。バイがブラックジャックでいうダブルに相当し、ツイストがヒット、スティックがスタンドに相当し、スプリットはそのままです。ブラックジャックの場合ダブルなら賭け金を倍にし、1枚だけカードを引いて勝負となりますが、ポンツーンのバイの場合はその後にもカードを引けます。またカードを何枚引いた後でもバイはできます。スティックは合計15以上のハンドで可能です。つまり14以下ですと強制的にツイストしなければなりません。またバイしても合計が14以下だったら強制的にツィストさせられます。スプリットは同じ数字であれば何回でも可能です。

 

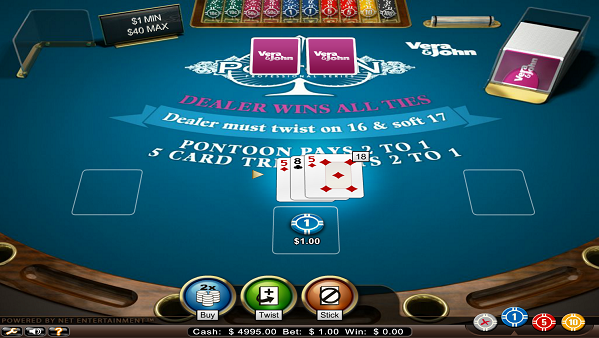
ツイストした後合計18になりましたので、ここでスティックしました。勿論スティックもバイもできますが21を超えてしまえばバーストで、プレイヤーの即負けとなってしまいます。また5枚のカードで21以下になれば5カードトリックと言ってプレイヤーの勝ちで2倍の配当となります。

 

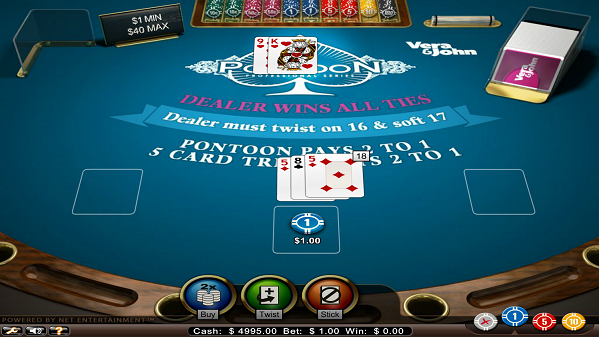
スティックしますと次は相手のアクションです。相手のホールカード(裏向きのカード)が表に返され、17以上になるまでツイストしなければなりません。(16以下は強制的にツイスト。)21を超えてしまえばバーストでプレイヤーの勝ちとなります。これで両者を比較し21に近い方が勝ちですが、同じ数ならディーラーの勝ちとなります。この場合は合計19ですので即スティックでディーラーの勝ちとなりました。

 

例1)

$10ベットしてポンツーンだったので、$20の配当($30のリターン)を得ることになりました。

 

例2)

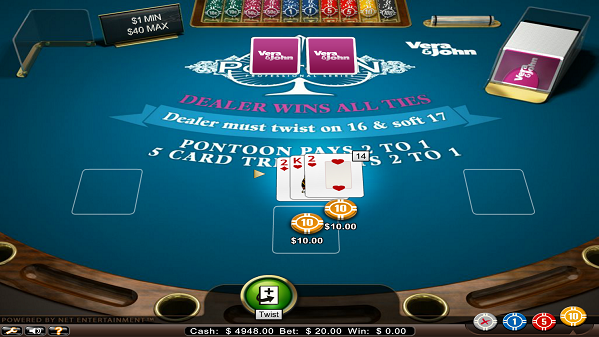
$10ベットしてバイしましたが、合計14ですので強制的にツイストしなければいけません。

 

例3)

数は同じ20ですが、同点なのでディーラーの勝ちとなりました。

 

例4)

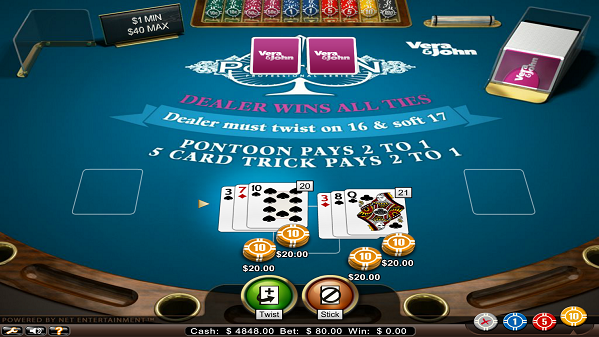
最初$20をベットし、3のペアでスプリットをし、それぞれでバイしました。

 

例5)

$10ベットしてバイをし、結果5カードトリックになりましたので、相手の数に関わらず即勝ちで、$40の配当($60のリターン)を受けました。

 

ポンツーンとブラックジャックの主な違い

相違点	ポンツーン	ブラックジャック
ディーラーの最初の2枚のカード	2枚とも裏向き	1枚表向きで1枚裏向き
引き分けの場合	ディーラーの勝ち	プッシュ(賭け金の払い戻され)
バイ(ダブル)	いつでもでき、その後もカードを引ける	3枚目のカードのみで有効で、それでスタンド
プレイヤーのツイスト(スタンド)	14以下なら強制的にツイスト	いつでもスタンドできる
2枚のカードがAを含む21でプレイヤー勝ちの場合	2倍の配当	1.5倍の配当
5カードトリック	2倍の配当	関係無し

 

ポンツーンとブラックジャックどちらが有利か

ポンツーンの場合、2枚のカードがAを含む21でプレイヤー勝ちの場合と、5カードトリックが、2倍の配当になるのが大きいです。しかしプレイヤーは14以下で強制ツイストしなければいけないためバーストしやすく、何よりも引き分けた場合プレイヤーの負けになってしまうのが大きすぎるため、ブラックジャックの方がプレイヤーに有利なゲームというのが私見です。

しかしルール説明によりますと、同じ6デッキで、ポンツーンの理論上の還元率は99.66%とあり、ブラックジャックですと99.54%とありますので、どちらが有利ということはほとんど無いようです。

いずれにしろ控除率が相当低くプレイヤーにとって旨味のあるカジノゲームと言うのは間違いないです。

 

戦略

ブラックジャックのディーラーのアップカードが見れないため、汎用基本戦略は使えません。また控除率があるため長くやっていれば確実に負けるゲームなのも言うまでもありません。

まずバイに関してですが、ディーラーのアップカードが見れないため基準となる対象が無く、どういう時にやればプレイヤーが有利なのか分からないのです。強いて言えば5カードトリックが確実なら絶対にやって下さい。他はプレイヤーの合計が10或いは11の時はやる価値があるかもしれませんが、それ以外はやらないのが無難だと思います。私は9でも試してみましたがいい結果にはなりませんでした。どのタイミングでバイするかは攻略のカギです。

合計15以上でスティックできるならソフトハンド(Aを含むハンド)を除き、してしまった方がいいです。さすがにそれ以上ツイストするとバースト率が高くなるからです。

スプリットは66、77、88、AAの時にすることをおすすめします。22、33は5カードトリックになる可能性があるため普通にツイストし、44は次に10の目を期待しやはりツイスト、55はやはり10の目に期待しダブル、66、77、88は次に10が出るとバーストしてしまいますので防衛の意味でスリプト、99、1010はスティック、AAは5カードトリックもあるため微妙ですが、スプリットしてポンツーンを狙いに行った方がいいと思いま。

ソフトハンドはなるべく低い方の目で考え5カードトリックを狙いに行って下さい。

 

例1)

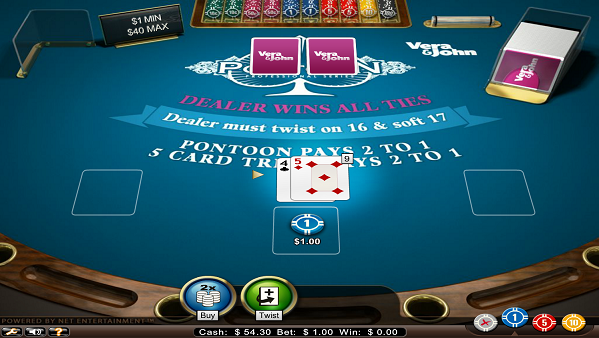
合計9で次のカードが10だとしたらバイでも良さそうだけど、ディーラーのカード情報が無いのでツイストが無難。

 

例2)

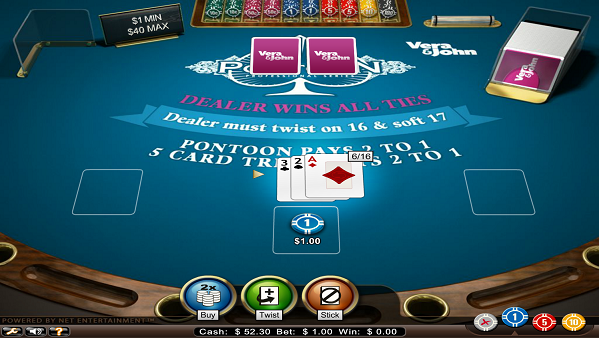
ソフト16ですが6の方を見てツイストします。

 

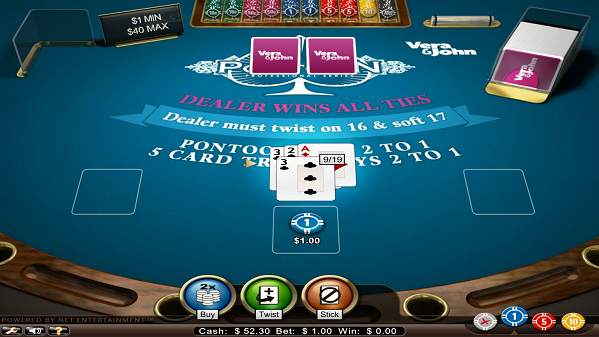
次に3が出てソフト19になりましたが、ここは9を見て5カードトリックになりますので絶対にバイして下さい。配当が4倍になります。

 

例3)

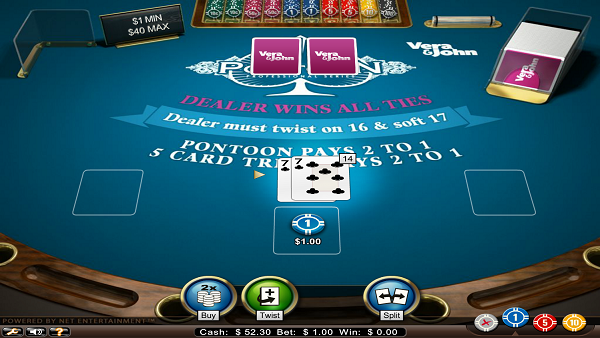
77で次に10が出るとバーストしますので、ここはスプリットします。

 

感想

以上の私が考えた戦略で試してみましたが、これに則っても$1賭けで5ハンドにつき$1の割合で負かされました(泣)。中々カジノの控除率を上回るのは難しいです。タイでも負けになるためブラックジャックよりよく負ける感じがしますが、5カードトリックのバイに旨味があるので増える時は美味しいです。体感的にも控除率でもポンツーンとブラックジャックはほぼ五分で、どちらがプレイヤーに有利とは言えない感じです。

 

どのオンラインカジノでできるか

ポンツーンは2019.6.7現在はどこのライブゲームにも無く、テーブルゲーム専用となっています。ベラジョンカジノ、888カジノ、ワンダリーノカジノではNetEnt社のものができ、ウィリアムヒルカジノクラブではPlaytech社のものができ、それぞれ賭け金が異なります。

配信会社	ゲーム名	賭け金	カジノ
NetEnt	Pontoon Pro	$1～40	ベラジョン、888カジノ
NetEnt	Pontoon Pro – High Limit	$25～500	ベラジョン、ワンダリーノ
NetEnt	Pontoon Low Limit	$0.1～5	ワンダリーノ
Playtech	ポンツーン	$0.5～30、$2～100	ウィリアムヒルカジノクラブ

 

888カジノやワンダリーノカジノのテーブルはベラジョンのテーブルと色違いです。

 

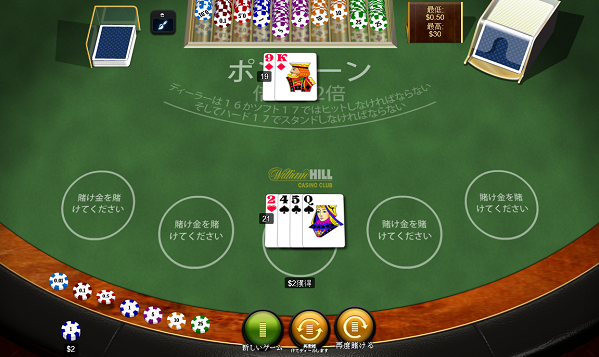
ウィリアムヒルカジノクラブのテーブルは動作が非常に早く、1ゲームの回転率がいいです。またヒット、スタンドとブラックジャックの用語でコマンド表示されます。

記事編集日 2018.4.27

ラスベガスをぶっつぶせに感銘を受けて、本当にカードカウンティングはこんなにも威力があるのかと思い、カードカウンティング入門という本を購入し実験してみました。

 

 

やり方

まずどのような実験をしたのか説明します。

最初に勝ちやすいカード構成を見ても分かる通り、Aと10のハイカードが多い方が勝ちやすいということになています。(本だとP72～74)

そしてカードカウンティングでより多くのアドバンテージを得るためにに、より少ないデッキ数を選ぶとあります。(本だとP148～149)

以上よりシングルデッキでIRCは0とし、カウント値0(52枚の状態)、＋12(2～7を2セット抜く40枚の状態)、－10(T、J、Q、K、Aを2セット抜く42枚の状態)でそれぞれ50ハンドづつシュミレーションしてみました。カウント値に関してはカウント値と期待値をご参照下さい。1ハンド毎にカードはよくシャッフルし、プレイヤーのアクションは汎用基本戦略に従うものとしました。スプリット後のダブルあり、インシュランスは取らないものとしました。

 

結果と考察

これが記録していたものです。以下結果をまとめ、考察しました。

 

1デッキ　IRC 0　カウント値 0(54枚)

プレイヤーバースト	9回
ディーラーバースト	9回
プレイヤーブラックジャック	4回
ディーラーブラックジャック	1回
プレイヤーダブル勝ち	3回
プレイヤーダブル負け	3回
ディーラーカード2枚で決着	16回

試行回数50ハンド。毎回$1ベットするとすると$＋6でした。

トータルが＋になりましたが、試行回数が50ハンドですのでブレの範疇だと思われます。

 

1デッキ　IRC 0　カウント値 12(42枚) 

プレイヤーバースト	5回
ディーラーバースト	10回
プレイヤーブラックジャック	3回
ディーラーブラックジャック	5回
プレイヤーダブル勝ち	2回
プレイヤーダブル負け	2回
ディーラーカード2枚で決着	31回

試行回数50ハンド。毎回$1ベットするとすると$＋0.5でした。

プレイヤーに相当有利なカウント値12の試行ですが、思ったほどの効果は現れませんでした。ハイカードが多く含まれているとディーラーのバースト率は上がるそうですが、カウント値0の状態とそれほどの差はないような感じです。

そもそも10カードが多いため、ディーラーが2枚でパットハンドになってしまう場合が多く、カウント値が0の時16回に対して、カウント値12は29回もありました。言い換えるとディーラーがスティッフハンド(12～16)になる場合が少ないということです。ちなみにカウント値－10では11回と大体予想していた通りの結果を得ました。

ブラックジャックの頻度は確かにカウント値0に比べやや多くなる感じですが、それがプレイヤーにくるとは限らず、今回はディーラーほ方が多かったです。大数の法則が働けばプレイヤーもディーラーも大体同じになり、配当が1.5倍の差分プレイヤーが利益を得るのは分かりますが、では大数とはどれくらいの数なのか？少なくとも試行回数が50ハンドではまだまだブレの範疇でした。

ダブルダウンに関してはハイカードが多くなるため、その機会がカウント値0よりも少なくなり、あまり恩恵に授かれない感じでした。

 

やっていて気づいたことなのですが、ハイカードが多いということはディーラーのバーストを際立たせるように、12以上はスタンドしたらその効果がより顕著になるのではないかと思い、それで50回の試行をやってみました。但しディーラーのアップカードがAの時は汎用基本戦略に従いました。

1デッキ IRC 0 カウント値 12　12以上はS

プレイヤーバースト	0回
ディーラーバースト	9回
プレイヤーブラックジャック	1回
ディーラーブラックジャック	5回
プレイヤーダブル勝ち	1回
プレイヤーダブル負け	0回
ディーラーカード2枚で決着	29回

試行回数50ハンド。毎回$1ベットするとすると$－8.5でした。

今回12以上はスタンドでしたので、プレイヤーのバーストは0となります。しかしディーラーのバースト率の変化はあまりないように感じました。

ブラックジャックの回数は今回はプレイヤーに悪く働きすぎました。これからも50ハンドというのは大数の法則にはほど遠いというのが分かります。ダブルダウンの機会はやはり少ないというのが改めて分かりました。

 

1デッキ　IRC 0　カウント値 －10(44枚)

プレイヤーバースト	6回
ディーラーバースト	10回
プレイヤーブラックジャック	0回
ディーラーブラックジャック	2回
プレイヤーダブル勝ち	3回
プレイヤーダブル負け	7回
ディーラーカード2枚で決着	11回

試行回数50ハンド。毎回$1ベットするとすると$－17でした。

ローカードが多いため、たくさんのカードを引くケースが多かったです。ディーラーの17～21に達する回数はカウント値0に比べて増えるそうですが、やはり試行回数50ハンドではあまり差はみられませんでした。寧ろ1回増えました。

しかしプレイヤーの17～21に達する回数も増えるのかプレイヤーのバースト率は下がっていました。ブラックジャックの総回数ははっきりとカウント値0に比べて少なくなるのが分かります。

またローカードが多いとダブルダウンできる機会がはっきりと多くなるのも分かります。

しかし3枚目のカードもローカードが出る可能性が高く、プレイヤーが相当負け越す結果となりました。ローカードが多く残る場合はどうもダブルダウンの勝負はしない方がいい感じです。

 

結論

カードカウンティングは理論上有効な手段だというのは分かりますが、それでも大数の法則が働かなければ相当にブレます。今回はそれぞれ50ハンドづつ試行しましたが、全然ブレの範疇で、カウント値が＋12でもプレイヤーに不利益な結果となりました。

使ったカードは全て見せて、カードは最後まで使いきるという条件ならいざ知らず、本当にカードカウンティングで勝てたのかな？という疑問すら残りました。

現在のライブブラックジャックはマルチデッキで、カットカードがシューの真中くらいにあるため、半分くらいのカードしか使われず、もっと偏りが起こりにくい状況です。こうなるとカードカウンティングで勝つのはほぼ絶望的という結論になってしまいます。

我々にとってMITのブラックジャックチームはもはや遠い夢の中の憧れの存在となってしまったのでしょうか。以下勝ちやすい理論と実際にはどうだったかをまとめておきます。

 

理論上の勝ちやすいカード構成(Aと10が多い状態)の理由と実際

1)Aと10の多い状態はナチュラル(ブラックジャック)が出易く、プレイヤーが勝った場合に支払いが1.5倍になるため。理論上は正しいが収束には大数の法則を必要とする。

2)ディーラーは17～21に達するまでヒットし続けなければならないため、ディーラーがスティッフハンド(12～16)の時はハイカードが多いほどバーストしやすくなる。しかしAと10が多い状態ではスティッフハンドになること自体が減る。

3)汎用基本戦略を見ても分かる通り、ダブルダウンの時プレイヤーに必要なカードはハイカード(Aと10)であるため、ハイカードが多い状態ほど勝ちやすい。しかしハイカードが多いとダブルダウンになること自体が減る。

4)77、88、99などの攻撃的なスプリットはやはりハイカードを必要とする。これは正しいと思うが、中々そういうスプリットになること自体が少ない。

5)ディーラーのアップカードがAで残りに10が多いと、やはりナチュラルになる可能性も高まるのでインシュランスが有益になる。これは正しいと思う。

まとめるとハイカード(A、10)が多い状態ではプレイヤー有利で、ローカード(2、3、4、5、6、7)が多い状態ではディーラー有利と言われていますが、実際には微差でプレイヤー有利か本当にその理論は正しいのか疑わしいレベル。

2018.3.7 編集

「ラスベガスをぶっつぶせ」は実話元に作り上げたアメリカ映画で2008年に公開されました。2週連続で興行収入1位を獲得し、同年日本でも公開されました。

 

 

ストーリー

「勝ったぞチキンディナーだ。」とはラスベガスで古くから伝わる言葉で、ビニオンズの中国人ディーラーが言い始めた言葉です。「あの晩僕はそれを14回も聞いた。」と主人公のベンが語るところから始まります。

 

マサチューセッツ工科大学(MIT)に通う秀才のベンは、ハーバード医科大へ行くための資金30万ドルを如何に捻出しようか、時給8ドルの洋服屋のアルバイトをしながら友人のジミーやマイルズと学生生活を送っていました。彼等は一緒にロボットの2.09大会で優勝を狙う間柄でもありました。

ある時数学の授業でミッキー教授が、ベンの感情に走らず論理で考える才能を見抜き、ミッキーとMITの学生で構成される大金稼ぎをもくろむブラックジャック必勝チームにベンを誘います。最初は断わったものの、思い憧れているチームの一員ジルに説得され心が動きます。

チームに加わったベンはもう特訓をし、カードカウウンティングをマスターするようになりました。チームは暗号を作り偵察役とプレイヤー役に分かれ、チームプレイでカウンティングをカモフラージュします。チームプレイが完成してきた頃いよいよ煌びやかなラスベガスへ乗り込みます。

 

最初は上手くいき瞬く間にベンは10万ドルの貯金を作ってしまいます。しかしやがてカジノの用心棒のコールの目に留まってしまいます。そしてブラックジャックで金稼ぎしていることをジミーやマイルズに隠していたため、やがて怪しまれて仲に亀裂が生じてしまいます。

しかし楽に金が稼げることを経験してしまったカジノの誘惑には勝てませんでした。稼ぐ金額も日増しに大きくなっていきました。何でも欲しい物は買え、ホテルの部屋も豪華スイートに、バーも学生ばかりのやぼなバーから豪華なバーへ、乗る車はリムジンへと変化していきました。

ベンの才能を嫉んだチームのフィッシャーは、ある時カジノで騒ぎを起こしてしまい、ミッキーから解雇通告を受け、チームから離脱してしまいます。ジルとは深い間柄になるも、ジミーやマイルズには友情の希薄性から見限られてしまいます。

 

このことがつっかえたのか、ベンはカジノでギャンブルをやってしまい大負けをしてしまいます。そしてミッキーの怒りを買いチームは一旦解散するも、ベンの呼びかけでジルとチョイとキアナは再び共に稼ぐことを決意します。この時ベンは既に目的の30万ドルは貯めていましたが、稼ぐことに取り憑かれてしまったのかカウンティングを止めようとはしませんでした。そして遂にコールにカウンティングの現場を捉えられてしまい、カジノ裏に連れて行かれて痛い目に遭わされてしまいます。

寮に戻ると単位不足による留年通達が届いており、部屋には隠しておいたお金がありませんでした。逆にジミーとマイルズは2.09大会で優勝し、その姿をベンは遠くで見守りました。そして今まで隠していた事を全てジミーに打ち明けます。

ミッキーには自分がバカなことをしたと謝り、再び組んで一儲けすることを提案します。ミッキーはこれに応じてチームを復活させ最後の大勝負に挑みます。ミッキーと組んだベンは仲間の協力もあって勝ちに勝ちまくります。しかしそれを見てたのがやはりコールでした。

 

チップを片付け一目散に逃げますが、コール一味は追いかけてきます。実はこれには裏取引があり、前回ベンがコールに捕まった時、ミッキーを呼び出すように言われていたのです。代わりに一晩稼がせてやるという条件でした。ミッキーは一人になった時、メダルがチョコだったことに気づきます。

ベンは本物のメダル持ってジルと逃げたかに思われましたが、最後に出てきたのはやはりコールで、そのメダルを置いていくように銃を見せられました。こうして2度までもベンは大金を奪われることになりました。

これらの話をハーバード医科大学の奨学金試験の面接官に打ち明けます。試験管の驚嘆した顔にはベンの輝かしい未来が感じられ幕を閉じます。

 

感想

カジノで大勝ちするというのは男のロマンですが、それを現実化したMITの学生達には尊敬の念を抱きます。ブラックジャックの1度使ったカードはデッキに戻さないため、残りのカードの偏りが生じ、そこを利用して勝ちやすいタイミングで大きく賭けるというのはよく思いついたなっと思います。またその実話を元にしてここまでのストーリを作り上げたのもさすがにアメリカ映画だなっという感じでした。

アメリカンジョークもたっぷり組み込まれ、友情の崩壊や恋愛と人間らしい場面を見せられるのも、月並みではありますがこの映画を魅力的な点にしているところだと思います。キラキラしたカジノの描写や敵役でもあるコールの存在なども如何にもカジノらしさを演出していると思いました。

1度は裏切られたミッキーとまた手を組むと見せかけて実は裏切るというのもこの手の映画にありがちな意外性を出していると思いました。これらのストーリが主人公の面接官への語りの一幕というのもよくある設定です。実にアメリカらしい映画で名作だと思いました。

「常に変数変換を考えろ。」と言う教授の言葉は名言だと思いました。麻雀にしろポーカーにしろこの要素があるから一見運ゲーのようで実力差が出るのですからね。

 

実話

ゲーミングリゾートであるモンテカルロで、MITのブラックジャックチームのアンディー、セミョン、ケイティーの3人は相当の大勝ちを積んだ後、屋根裏部屋へ連れて行かれ、警察によって執拗な尋問を受け、モンテカルロでカードカウンティングは違法であることを警察に告げられました。

しかし3人は告訴されず、勝った金も没収されませんでした。警察のエスコートの元「2度とこの国へ戻ってくるな。」と告げられ国境まで送り届けられたとのことでした。

 

カードカウンティングは違法か？

アメリカではカードカウンティングは違法ではありませんが、世界には別の見解を持つ政府も存在するようです。