楽しく遊べるオンラインゲーム実戦記

ブラックジャックが他のカジノゲームと大きく異なる点は各々試行が従属事象であるという点です。

このためカウンティングがとても有用で、昔からブラックジャックの攻略法として様々な人が試みてきました。

マサチューセッツ工科大学の3人がラスベガスに乗り込んで大勝したのはあまりにも有名なエピソードで、多くのプレイヤーにとっての憧れの存在であり、カジノにとっては恐怖の存在であります。

ここではこのカウンティングがオンラインカジノでできないのかを検証してみたいと思います。

従属事象の妙味

オンラインカジノのテーブルゲームのブラックジャックは1回毎に使用済みのカードがデッキに戻されシャッフルされるため独立事象ですが、ライブディーラーのブラックジャックは使用済みのカードをデッキから取り除くため、従属事象と言えます。

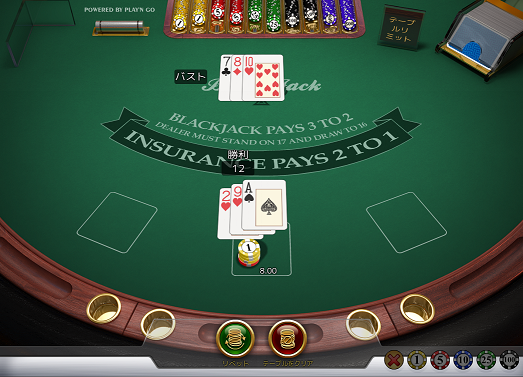
テーブルブラックジャックはこうして1回のゲームが終わると、使用されたカードはデッキに戻されてシャッフルされた状態から始まります。

しかしライブブラックジャックの場合は使用されたカードはデッキに戻されず、ディスカードホールダー(左のボックス)へ入れられます。

よってライブブラックジャックの場合はネクストゲームでは、シューのデッキカードの構成が変わってしまっているということになります。(使われたカードは含まれていないため。)

こうなると残りのカードに偏りができることになります。これが従属事象の妙味なのです。

勝ちやすいカードの構成

次にプレイヤーにとって有益なカード構成と不利益なカード構成を考えてみます。

結論から言ってしまえば以下の理由により、Aと10のハイカードが多い状態はプレイヤーにとって有利といえ、それ以外のローカードが多い状態はプレイヤーにとって不利といえます。

1)Aと10の多い状態はナチュラル(ブラックジャック)が出易く、プレイヤーが勝った場合に支払いが1.5倍になるため。

2)ディーラーは17～21に達するまでヒットし続けなければならないため、ディーラーがスティッフハンド(12～16)の時はハイカードが多いほどバーストしやすくなる。

3)汎用基本戦略を見ても分かる通り、ダブルの時プレイヤーに必要なカードはハイカードであるため、ハイカードが多い状態ほど勝ちやすい。

4)77、88、99などの攻撃的なスプリットはやはりハイカードを必要とする。

5)ディーラーのアップカードがAで残りに10が多いと、やはりナチュラルになる可能性も高まるのでインシュランスが有益になる。

つまり残りのカード構成にAと10のハイカードが多い場合はプレイヤー有利と判断して大きく賭け、逆にローカードが多い場合はプレイヤーに不利と判断して小さく賭けるのがブラックジャックのカードカウンティングを利用した攻略法になります。

カウント値と期待値

ではどれくらい影響するのか見てみます。以下はシングルデッキからカードを1枚取り除いた後の相対価値になります。

ベンチマークのシングルデッキの元々の期待値は－0.02%であるため、例えば5を1枚取り除けば期待値は＋0.65%に向上したことになります。Aと5を取り除けば、－0.59＋0.67－0.02＝＋0.06%になったことになります。

これを踏まえた上でカウント値を以下のようにします。

IRC(初期設定のランニングカウント)の値に関しては以下の公式に従います。

IRC=4-(4×デッキ数)

※例えば8デッキの場合は、4-(4×8)＝－28となります。

そしてデッキに関わらず全てのカウントをし終えるとRC＝4となります。

次にキーカウントを以下のように決めます。キーカウントとはプレイヤーのアドバンテージが＋になった時のカウント値をいいます。

つまりキーカウントに達した時点で大きく賭け、達していない時は小さく賭ければ、ユーザーはこのゲームのアドバンテージを得ることができます。

賭け額の単位をユニット数で表せば期待値(%)は以下の通りになります。

つまりデッキ数が小さいほど、ユニット幅が大きいほど期待値は大きくなります。

カウンティングの実践結果と考察

上のルールに従いまして、ベラジョンカジノのカジノ・パリスにてカウンティングを実践してみました。

カジノ・パリスのルールは8デッキでスプリット後のダブルはなしです。

期待値を計算しますと、－0.02(ベンチマーク)－0.55(8デッキより)＝－0.57 となります。

8デッキなのでIRC=－28、キーカウントは－6となります。

当然ながらカウントは新しいデッキになった時から数えるものとします。

大体1デッキ辺り13～16ラウンドで終了してしまいます。

理由はカットカードが大体シューの真中辺りに入っているからです。赤いカードがそうですが、これが出るとこのラウンドが最後で、次のゲームから新しいデッキ(後ろに控えている青いカード)になります。

全体のデッキのカードの使われる割合をペネトレーションといいますが、これが50%くらいしかないのです。

カットカードがもっと深い位置にあればいいのですが、これがシューの真中辺りですと8デッキでは、カードの偏りが強く起こる前に終了してしまう感じです。

結果としてキーカウントの－6に達する前に終了ということになります。

実践でも最も近づいたのは－8ですが、－6に達することはありませんでした。

考えてみますと、オンラインカジノですからカウントもリアルに比べて容易ですので、ユーザーにとって期待値の高い状況をわざわざオンラインカジノが作るわけがないですよね。カードの偏りが起こる前にそのデッキを終了してしまうというのがオンラインカジノ側のブラックジャックのカウンティングに対する対策でした。

カウンティングでより多くのアドバンテージを得るために

最後にランドカジノのブラックジャックのカウンティングでより多くのアドバンテージを得る条件をまとめておきたいと思います。

○より少ないデッキ数を選ぶ(少ないデッキの方がカードの偏りは起こりやすく、プレイヤーに有利な状態つまりハイカードが多い状態になることが多いです。)

○ベットスプレッドを大きくする(有利な時と不利な時に賭ける金額の差が大きいほど利益も大きくなります。)

○より深いペネトレーションを求める(使われるカードの割合が多いほどRCはピボットポイントに辿り着く可能性は高くなります。)

○少人数のテーブルを選ぶ(少人数プレイの方がデッキ毎のゲーム数が多くなるため、有利な状態で賭けれるタイミングが多くなります。)

そしてこれは忘れてはいけないのですが、カウンティングをしても負ける時は負けます。あくまで期待値が高いというだけであって、確率の低いこともたまには起こりえます。

出禁

カジノにも出禁というものがあります。カジノ側にとって不利益だと思う人間を出入り禁止にすることです。特にブラックジャックはカウンティングによって有利な状態か不利な状態かを測れてしまうため、カウンティングをやっていると思うプレイヤーがいれば、出禁にしたり、もっと不利な状況(デッキを増やしたり、カッとカードを浅くしたりだとか)にしたりする場合があります。ですのでカードカウントをする時は何気ないふりしてカウントしなければなりません。間違っても口に出したりしてはいけません。

カジノの豪華な外観や内装、人件費、株主や投資者への支払い、カジノ部門意外(レジャー施設)の赤字の埋め合わせは当然ゲームの売り上げから賄われるため、カジノ側としてもゲームには負けられないのです。全てのカジノゲームはハウス側に期待値がプラスになるようにできており、長期的にはやはりその期待値通りに収束してしまいますが、ブラックジャックだけはカードの偏りによってはその限りではありません。よってハウスからすれば、カウンティングは天敵なのです。このためカウンティングをやってるような人はいないか、ピットのスタッフは常に見張り続けています。

しかしカウンティングをしているプレイヤーの全てが期待値がプラスにできているわけではなく、数え間違いや大きなベットの躊躇いなどから中々勝てない人もいます。カジノ側もこういう人達は問題にせず、要はカジノに勝つ腕を持っているかどうかで見極めるそうです。面白いことにプロのカウンターは周囲に自分の腕を見せるために、わざと出禁になる者もいるそうです。

ブラックジャックの現状と基本戦略

ブラックジャックはカジノゲームの中でも最も人気の高いテーブルゲームで、毎年900億ドル近くが賭けられていると言われています。アメリカの人口から考えて1人当たり毎年275ドルも賭けているのです。

しかし結果は残念ながら思わしいものではなく、毎年20億ドルほどカジノ側が勝っているというのが現状です。

ブラックジャック攻略と言えばまずカードカウンティングが思い浮かばれますが、ここではそれ以前に遡り、基本戦略を見ていこうと思います。

基本戦略(ベーシックストラテジー)というのは、残りのデッキの状態に関係なく、プレイヤーの最初の2枚のハンドと、ディーラーのアップカード(最初の表向きのカード)から、期待値に基づいた最善のアクションを取っていく戦略になります。

カードカウンティングがゲーム間が従属事象なのに対して、基本戦略は独立事象ということになります。

基本戦略の歴史

1950年代当時のブラックジャックプレイヤーのプレイはとてもお粗末なもので、12や13でのヒットは普通、8のスプリットはほとんど見られずスプリットされるものは10が多い、A5などのソフトトータルでのダブルはまず見られない、といったものでした。

1953年になってボールドウィン、カンティー、マイゼル、マクダーモットの4人の陸軍数学者がブラックジャックの研究をはじめ、3年間の膨大な計算結果を元に発表されたのが基本戦略(ベーシックストラテジー)というものです。『Journal of the American Statistical Association』の「The Optimum Strategy in Blackjack」の中でoptimum strategyとして紹介しています。

これはとても優秀でシングルデッキでは期待値は0%(トントン)になるまでに至りました。それまで最も最適な戦略でも－3.6%だったので飛躍的な向上と言えます。発売当時その本を手に取ったソープ教授がラスベガスの旅行中に実践検証してみたら、初期投資は消えなかったという結果になっています。

その後何人もの人がプレイを検証し、設定やルールに対応していき、いくつもの基本戦略が生まれましたが、そのほとんどはシングルデッキかマルチデッキ対応のものでした。どの基本戦略でも誤差は0.03%と非常に小さいです。ここではシングルからマルチデッキまで全てに汎用できる戦略を紹介します。

汎用基本戦略

使用されるカードがランダムでカウンティング等の情報がない時、これに従うことにより最もプレイヤーの成績を高めてくれる戦略。期待値0%で理論上はほぼトントンになります。

Sp：スプリット、S：スタンド、H：ヒット、D：ダブル、Su：サレンダー、Su/H：サレンダー不可のルールではヒット、D/H：ダブル不可のルールではヒット、D/S：ダブル不可のルールではスタンド

※どんな場合でもインシュランスは取らない。

この基本戦略には以下の特徴があります。

スプリットに関しては主にディーラーのアップカードが弱い時(6以下)に行われ、Aのペアと8のペアは常にスプリットする。Aのペアは攻撃的な意味合いを持ち、8のペアは半端な16を避けるためのディフェンス的な意味合いを持つ。

4、5、10のペアはどんな場合でもスプリットしないが、これはハンドの価値を下げないため。

ダブルに関しては、プレイヤーが一枚引いて完成されたハンドの勝算が高めの時に行う。

ヒットとスタンドに関しては、プレイヤーがスティッフハンド(合計12～16)で、ディーラーのアップカードが強い時(7以上)は、ディーラーがパットハンド(17～21)になる可能性が高いとみなしてヒットする。逆に弱い時はディーラーがバーストしてくれることに期待してスタンドする。

実際は細かいルールによって期待値が微妙に変わるため、以下の条件に合わせて修正します。(初期値のベンチマークの－0.02%から修正)

ベンチマーク：ラスベガスストリップのゲームと言われるルールで、シングルデッキ、最初の2枚ならどんなハンドでもダブル可能、ペアAのスプリット後にはカードが1枚ずつ配られる、ディーラーはソフト17をスタンド、サレンダーなし。カードが1枚も出ていない状態のゲームでは期待値は－0.02%で、この状態から修正していけばよい。

この修正表で気づくことは、まずはデッキ数が多くなればなるほど期待値が下がるということです。これはシングルデッキの方が1枚取り出された後の残りのカードへの影響力が大きいため、デッキ数が増えるほどその有利差が母数によってかき消されてしまうためです。

例えばプレイヤーが4、6のカードでディーラーのアップカードが5の時、プレイヤーはAか10を引くことを望むと思いますが、シングルデッキの時は20/49(0.408 )の確率なのに対して8デッキの時は160/413(0.387)まで下がってしまいます。

そしてプッシュはディーラーの勝ちとするルールは最悪で、長期的に見てプレイヤーが勝つことはまず不可能と言えます。このルールはチャリティーイベント等でよく採用されます。

なぜインシュランスは取らないのか？

インシュランスは基本的にどの戦略でも取りません。なぜなら、インシュランスの結果自体はメインハンドになにも影響を及ぼさず、完全にサイドベットでその期待値は完全にマイナスだからです。

4/13(2)＋9/13(－1)＝－1/13

単純計算で1回インシュランスをやる毎に、インシュランス代の－1/13が無くなる計算になります。

※しかしカウンティングができる場合はデッキに10が多く残っている場合はインシュランスが有効になてきます。

この汎用基本戦略で重要な所は、感情や結果は一切交えず、忠実にこの通りにプレイするということです。例えば16対7が3回連続で出て、3回ともバーストに終わったとしても、次に16対7が出ればやはりヒットしなければいけないのです。長期的に正しいプレイをするということが重要なのです。

汎用基本戦略の実戦

それでは汎用基本戦略をエンパイアカジノで実践してみます。

これがエンパイアカジノのテーブルゲームのブラックジャックのルールです。

そしてラウンド毎にカードはシャッフルされます。

これに合わせて期待値を修正してみます。

－0.02－0.53－0.03＋0.13＝－0.45%となります。

つまりこれは100ドルベットすると0.45ドル無くなる計算で、1000ドルベットすると4.5ドル無くなる計算です。

では1ドル賭けで上表に従い1000ドルほど賭けてみます。

これが初期資金です。少し少ないですが、4.5ドルしか無くならない計算ですので、これで事足りるはずです。

第1戦目

プレイヤーハード14対ディーラー7のアップカードです。上表に従いヒットします。

5を引いてハード19になりましたのでスタンドします。

ディーラーは4、5、10と引いてバーストとなりプレイヤーの勝ちとなりました。

以下こんな感じで続けます。

第15戦目

プレイヤーハード16対ディーラー9のアップカードで、上表に従ってヒットしなければなりませんが、16でヒットするのはやはり辛いところです。

幸いにも引けたカードは3だったのですが・・・・

ディーラーの引いたカードはAで負けてしまいました。

以下は戦績表です。

いざ実践してみたのですが、最初は記入ミスが多く帳尻が合いませんでしたので、$65.33から改めて始めました。

$1ずつ賭け、ダブルは$2という計算です。

そして最終的には$58.33になりました。

65.33－58.33＝$7となり大体誤差の範囲だと思います。

結果を集計しますとこんな感じになります。尚ミス(アクションによるもの)が4回ほどありましたが、2回負けて2回勝ったのでチャラとします。

以下はディーラーのアップカード毎のバースト数です。

アップカード10はT、J、Q、Kの4種類なので相対的なバースト数は9くらいだと思います。アップカード9でのバースト数は少し多いものの、大体6と7が境界で、アップカード7からバースト数が少なくなってることも分かります。そしてアップカードAになると極端にバーストしなくなることも分かります。

考察

やってみて気づいたことですが、やはりプレイヤーがバーストして負けるケースが圧倒的に多い感じがします。取り扱うハンドはほとんどがハードハンドですので、表のハードハンドの部分はやっていく中に覚えてしまいます。逆にダブルになった時は、負けよりも勝ちの方が圧倒的に多いです。これとプレイヤーのブラックジャックの1.5倍の配当でうまく帳尻があってるんだなという気がします。

$65.33が原点ですと、$80を超えたり、$40付近になってしまったりとこれくらいの変動幅はありました。

またこの実践を通して予想外に大きく負けたわけではないので、このゲームに仕組まれた意図といったものもないのがわかりました。

汎用基本戦略は決して勝てる戦略ではありませんが、これに従えば相当ゆっくり負けていくというのが分かりました。

ここ最近になってビットコインが注目を集めるようになりました。

ビットコインというのは仮想通貨で中央銀行が存在せず、発行を司る組織や流通を管理する組織も存在せず、ブロックチェーンの仕組みによって自律性を持っている通貨になります。

2008年10月に中本哲史氏がビットコインのアイディアをネットで発表して、僅か3ヶ月後の2009年1月にはビットコインの理論を実現するためのソフトウェアがオープンソースで開発・公開され、そしてすぐに最初の取引が行われています。

誰の手にも委ねられない通貨ということにより価値の普遍性が認められたり、また介在者がいないことより流通の手数料が破格に安いという大きなメリットがあるからです。

これは2017年8月23日時点のビットコインの為替相場ですが、1ビットコイン(BTC)が30万6千849円というレートになっており、去年の9月、10月頃(6万ちょい)と比べて5倍近くも跳ね上がっていることが分かります。

まだ出来たての通貨で円やドルと比べてお世辞にも流通性がいい通貨とは言えず、このように投機の激しい通貨となっています。

また仮想通貨であるため現物の紙幣は存在せず、たた記録のみの通貨ですから、それらが無くなれば一気に無意味なものになってしまうというリスクもあります。

今のところは処理スピードが遅いという点を除き問題はありませんが、この先どんどん広まるにつれて何かしらの課題は必ず見つかると思います。

現在はこの処理スピードの解決をめぐり関連団体の利害が一致せず、事業者の対立により基幹システムが分裂しコインが失われる恐れが生じたことから、ビットコインの取引所13社は、利用者の資産を保護し混乱を回避するためビットコインの入出金を一時停止する措置にまで踏み切りました。

とはいうものの私の利用しているBitflyerはまだ入出金やビットコインの取引、ビットコインの送付ができています。

このビットコインですが、これが意外とオンラインカジノをはじめとするオンラインゲーミングに相性がいいのです。

理由は手数料が破格に安いことです。

Bitflyerへの入出金は数百円ほど掛かってしまいますが、ビットコインの取引手数料は無料、ビットコインでのオンラインカジノへの入出金は等価交換で手数料は無料ということになります。

今まではネッテラーやエコペイズを介在しなければならないため、為替手数料や引き出し手数料が高すぎて、勝ってもあまり利益を出しにくい感じでした。

しかしビットコインの場合はこれらがほとんど数百円くらいのただに等しい金額になるところがあり難いところです。

ただこれだけ投機性の激しい通貨ですから、少しスプレッドが大きいのが気になるところです。

これですと1ビットコインの購入価格が30万8千255円、売却価格が29万6千362円ということになります。

FXのドル/円の0.3銭というわけにはいきません。

まあほぼ1年前に比べて5倍も価値が上がるくらいの通貨で、ドルや円と流通量が全然違いますのでこれは仕方のないところです。

ビットコインは0.00000001BTC(約3銭)から取引できますので試してみて下さい。

ビットコインの使えるオンラインカジノはベラジョンカジノになります。